Алгебра 7 клас

Вправа 203

Умова:

У деякому місті з будь-якої станції метро можна доїхати до будь-якої іншої станції (можливо, з пересадками). Доведіть, що існує станція, яку можна закрити (без права проїзду через неї), і при цьому з будь-якої станції з тих, що залишилися, можна буде доїхати до будь-якої іншої.

 

Відповідь:

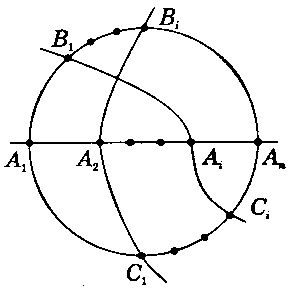
Щоб доїхати з будь-якої станції метро до будь-якої іншої (можливо, з пересадками), зв'язки (тобто рейкові колії) між станціями будуються таким чином, що є щонайменше дві станції (A₁, A_n), в яких сходяться три колії в кільцевому та радіальних напрямах (зі станцій, приміром, А_і, В_і і С_і чи зі станцій А_і, В_і та С_і). При закритті будь-якої зі станцій (А₁ чи А_n) залишаються вільними дві колії, якими можна доїхати до будь-якої станції (приміром, при закритті А₁ зі станції В₁ до станції С₁ через А_і або (при закритті А_n) зі станції В_і до станції C₁ через А₂). Аналогічно розглядаються випадки при закритті будь-якої станції метро на кільцевому чи радіальних напрямах.