Алгебра 7 клас

Вправа 305

Умова:

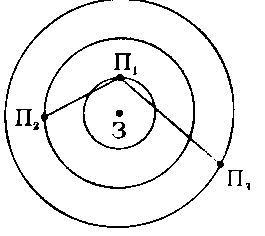
Навколо зорі обертається кілька планет, відстані між якими не змінюються та є попарно різними. На кожній планеті перебуває один астроном, який вивчає найближчу планету. Доведіть, що існують дві планети, на яких астрономи вивчають один одного.

 

Відповідь:

Для доведення достатньо розглянута щонайменше три планети. Нехай навколо зорі (3) обертаються планети П₁, П₂, П₃. Оскільки відстані П1, П2, П3 (за умовою) не змінюються і є попарно різними, то очевидно, що або відстань П1, П2 або відстань П1, П3 є коротшою, тобто або планета П₂, або планета П₃ знаходиться найближче до планети П₁ - а це якраз створює ситуацію, що астроном на планеті П₂ або астроном на планеті П₃ зможе вивчати планету П₁. У свою чергу, астроном на планеті П₁ отримує найкращу можливість для вивчення або планети П₂, або планети П₃. В обох випадках, отже, маємо дві планети, на яких астрономи вивчають один одного, що й потрібно довести.