Алгебра 7 клас

Вправа 498

Умова:

У турнірі, організованому за олімпійською системою (той, хто програв, - вибуває), беруть участь n тенісистів. Яку кількість матчів треба провести, щоб виявити переможця турніру?

 

Відповідь:

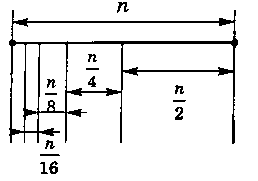
Аби тенісисти перебували в однакових справедливих умовах, очевидно, їхня кількість на кожному етапі розіграшу повинна бути парним числом (інакше один із тенісистів на певному етапі розіграшу за олімпійською системою з вибуванням повинен зіграти більшу кількість матчів - але це в принципі не так і важливо). Отже, кількість матчів дорівнюва-

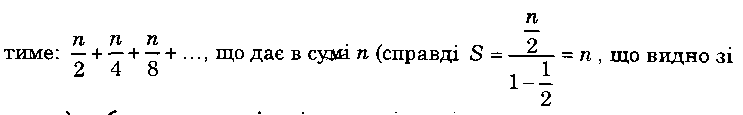
схеми), тобто загальна кількість матчів дорівнювала б загальній кількості тенісистів. Але фінальний (заключний і останній) матч визначає одного переможця із двох тенісистів. Таким чином, загальна кількість матчів, проведених усіма тенісистами, становитиме (n - 1) матч, де n - кількість тенісистів.
Для розв'язання цієї задачі можна скористатися таким нестандартним підходом. До заключного (фінального) поединку прийдуть тенісисти, один із яких повинен був виграти в половини учасників (без нього самого), тобто матчів будо n/2 - 1, а другий - теж програти в другої (іншої) половини учасників (теж без нього самого), тобто матчів буде n/2 - 1. Отже, загальна кількість проведених матчів до фінального матчу становитиме n/2 - 1 + n/2 - 1 = (n - 2) матчі. Фінальний матч "додає" ще один матч до загальної кількості, тобто матиме n - 2 + 1 = (n - 1) матч.
Можемо вказати ще Й на такий «нетривіальний» крок у розв'язанні. Оскільки будь-який конкретний тенісист виграти може скільки завгодно матчів, а програти тільки один раз (у системі з «вибуванням») (саме так, як і у повсякденному житті - жити можна скільки завгодно, а померти лише один раз, тобто загальна кількість жителів нашої рідної планети за всі часи, як це не парадоксально, визначається їхньою кільки «смертей»), то загальна кількість матчів визначається кількістю Щ граних матчів або, що те саме, кількістю «програних» тенісистів, то до останнього (фінального) матчу між двома тенісистами кількість програних матчів становитиме (n - 2). Фінальний матч «додає» ще один заключний акорд - «програний» матч і, отже, загальна кількість матчів становитиме
(n - 2 + 1) = (n - 1) матч.