Мерзляк Полонський Геометрія 7 клас решебник

Вправа 126

 

Умова:

На рисунку 105 BF ┴ AC, BD ┴ BK. Доведіть, що ∟ABD = ∟FBK.

 

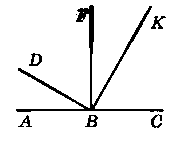
Відповідь:

Дано: DF ┴ AC, BD ┴ ВК. Довести: ∟ABD = ∟FBK.
Доведення: За умовою BF ┴ АС, тоді ∟ABF = ∟FBC = 90°.
BD ┴ Btf, тоді ∟DBK = 90°. Нехай ∟FBK = х, тоді за аксіомою вимірювання кутів маємо:
∟FBC = ∟FBK + ∟KDC, ∟KBC = ∟FBC - ∟FBK, ∟KBC = 90° - x.
Аналогічно, ∟DBK = ∟DBF + ∟FBK, ∟DBF = ∟DBAT - ∟FBK,
∟DBF = 90° - x.
∟ABF = ∟ABD + ∟DBF, ∟ABD = ∟ABF - ∟DBF, ∟ABD = 90° - (90° - x) =
= 90° - 90° + x = x. Отже, ∟ABD = ∟FBK. Доведено.