Геометрія 7 клас
Вправа 128
Умова:
Із вершини кута ABC, який дорівнює 70°, проведено променв BD i BF так, що BD ┴ BA, BF ┴ BC, промені BD i ВС належать куту ABF. Знайдіть кути DBF i ABF.
Відповідь:
Дано: ∟ABC = 70°, BD ┴ BA, BF ┴ ВС.
Промені BD i ВС належать ∟ABF. Знайти: ∟DBF, ∟ABF.
Разв'язання: BD ┴ BA, тоді ∟ABD = 90°, BF l ВС, тоді ∟FBC = 90°.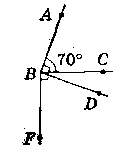
За аксіомою вимірювання кутів маємо:
∟ABD = ∟ABC + ∟CBD, ∟CBD = ∟ABD - ∟ABC,
∟CBD = 90° - 70° = 20°, ∟CBD = 20°.
Аналогічно, ∟FBC = ∟FBD + ∟DBC, ∟FBD = ∟FBC - ZDBC,
∟FBD = 90° - 20° = 70°. ∟ABF = ∟ABD + ∟DBF, ∟ABF = 90° + 70° = 160°. ∟ABF = 160°.
Biдповідь: ∟DBF = 70°, ∟ABF = 160°.
Повідомити про помилку
Обгрунтуй, що саме не так!




