Геометрія 7 клас решебник відповіді гдз

Вправа 152

 

Умова:

Промінь BD розбиває кут ABC, який дорівнює 72°, на два кути ABD і CBD так, що ∟ABD = 5∟CBD. Промінь ВК проходить так, що промінь ВА є бісектрисою кута DBK. Визначте градусну мipy та вид кута DBK.

 

Відповідь:

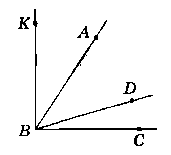
Дано: ∟ABC = 72°, BD проходить між сторонами ∟ABC.
∟ABD = 5∟DBC. ВА - бісектриса ∟KBD. Знайти: ∟DBK.
Розвязання:
Нехай ∟DBC = х, тоді ∟ABD = 5х.
За аксіомою вимірювання кутів маємо: ∟ABC = ∟ABD + ∟DBC.
Складемо i розв'яжемо рівняння:
х + 5х = 72; 6х = 72; х = 72 : 6; х = 12.
∟DBC = 12°, ∟ABC = 5 • 12° = 60°.
За умовою ВА - бісектриса ∟KBD.
За означенням бісектриси кута маємо:
∟KBD = 2∟ABD, ∟KBD = 2 • 60° = 120°. ∟KBD - тупий.
Bidnoeidb: ∟KBD = 120° - тупий.