Геометрія 7 клас
Вправа 172
Умова:
На сторонах кута з вершиною в точці В позначено точки A i С, а на його бісектрисі - точку D таку, що ∟ADB = ∟CDB.
Доведіть, що АВ = ВС.
Відповідь:
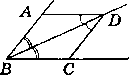
Доведениях Нехай ∟B дано за умовою, BD - бісектриса ∟B.
Розглянемо ∆АВD i ∆CBD.
1) ∟ABD = ∟CBD (за властивістю бісектриси);
2) ∟ADB = ∟CDB (за умовою);
3) BD - спільна.
Отже, ∆ABD = ∆CBD за II ознакою рівності трикутників, тоді АВ = ВС.
Повідомити про помилку
Обгрунтуй, що саме не так!




