Геометрія 7 клас гдз

Вправа 212

 

Умова:

Трикутник ABC - рівнобедрений з основою AC, BD - його бісектриса, DM - бісектриса трикутника BDC. Знайдіть кут ADM.

 

Відповідь:

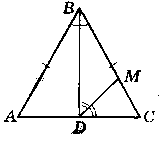
Дано:
∆АВС - рівнобедрений, АС - основа, BD - бісектриса ∆АВС,
DM - 6iceктриса ∆BDC. Знайти: ∟ADM.
Розв'язання:
BD - бісектриса ∆АВС. За властивістю рівнобедреного трикутника
маємо BD - медіана, бісектриса, висота. BD - висота.
За означениям висоти трикутника маємо BD ┴ AC, ∟ADB = ∟BDC = 90°.
За умовою DM - бісектриса ∆BDC, ∟DBM = ∟MDC = ∟BDC : 2 = 90° : 2 = 45°.
За аксіомою вимірювання кутів маємо
∟ADM = ∟ADB + ∟BDM, ∟ADM = 90° + 45° = 135°.
Biдповідь: 135°.