Геометрія 7 клас відповіді гдз
Вправа 219
Умова:
У рівнобедреному трикутнику ABC з основою АС на медіан BD позначили довільну точку М.
Доведіть, що: 1) ∆АМВ = ∆СМВ; 2) ∆AMD = ∆CMD.
Відповідь:
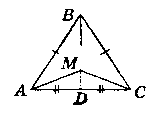
1) Дано:
∆АВС - рівнобедрений, АС - основа, BD - медіана, М є BD.
Довести: ∆АМВ = ∆СМВ.
Доведення:
1) За умовою ∆АВС - рівнобедрений, тому АВ = ВС.
2) BD - медіана. За властивістю медіан рівнобедреного трикутника маємо
BD - медіана, бісектриса.
За означениям бісектриси кута трикутника маємо
∟ABM = ∟CBM.
3) ВМ - спільна сторона. ∆АМВ - ∆СМВ (за I ознакою piвності трикутників). Доведено.
2) Довести: ∆AMD = ∆CMD.
Доведення:
Розглянемо ∆AMD i ∆CMD.
1) MD - спільна сторона.
2) За умовою BD - медіана у ∆АВС, тоді за означениям медіани трикутника маємо AD = DC.
3) За властивістю медіани трикутника маємо BD - висота, тоді BD ┴ АС, ∟MDA = ∟МОС = 90°.
∆AMD = ∆CMD (за I ознакою piвності трикутників). Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




