з геометрії 7 клас решебник

Вправа 220

 

Умова:

Доведіть, що бісектриси рівнобедреного трикутника, проведені з вершин кутвв при ocнові, piвні.

 

Відповідь:

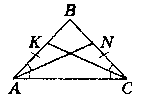
Дано:
∆АВС - рівнобедрений, АС - основа, AN - бісектриса ∟BAC, СК - бісектриса ∟ACB.
Довести: СК = AN.
Доведення:
Розглянемо ∆АКС i ∆CNA.
1) АС - спільна сторона.
2) За умовою ∆АВС - рівнобедрений,
тому ∟CAK = ∟ACN (кути при основі рівнобедреного трикутника).
3) AN - бісектриса ∟BAC. За означениям бісектриси кута трикутника
маємо ∟BAN = ∟CAN = 1/2∟BAC.
Аналогічно, СК - бісектриса ∟ACB. Тому ∟ACK = ∟KCB = 1/2∟ACB.
Тоді ∟NAC = ∟KCA.
∆АКС = ∆CNA (за II ознакою piвності трикутниюв).
Тому AN = СК (як piвні відповідні елементи рівних фігур). Доведено.