Геометрія 7 клас решебник відповіді гдз

Вправа 227

 

Умова:

На продовженнях сторін АВ, ВС, АС рівностороннього трикутника ABC (рис. 164) за точки А, В i С відповідно відклали piвні відрізки AD, BK i СЕ.  Доведіть, що трикутник DEK piвносторонній.

 

Відповідь:

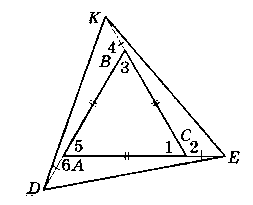
Дано:
∆АВС - рівносторонній, Е є АС, К є СВ, D є АВ, ДА = СЕ + ВК.
Довести: ∆DKE - рівносторонній.
Доведення:
1) За умовою ∆АВС - рівносторонній. ∟1 = ∟3 = ∟5 = 60; АВ = ВС = АС;
∟1 i ∟2, ∟3 i ∟4, ∟5 i ∟6 - суміжні за теоремою про суміжні кути маємо
∟2 = ∟4 = ∟6 = 180° - 60° = 120°.
2) За умовою AD = ВК = СЕ.
3) За аксіомою вимірювання відрізків маємо АЕ = СК = BD.
∆DAE = ∆ЕСК = ∆KBD (за I ознакою piвності трикутників).
DE = DK = КЕ (як piвності відповідних елементів рівних фігур).
Тому ∆DKE - piвносторонній. Доведено.