з геометрії 7 клас відповіді

Вправа 234

 

Умова:

У трикутнику ABC відомо, що ∟ACB = 90°, ∟A = ∟B = 45°, СК - висота. Знайдіть сторону АВ, якщо СК = 7 см.

 

Відповідь:

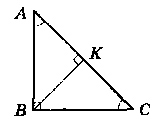
Розв'язання:
Нехай дано ∆ABC, ∟АСВ = 90°,
∟A = ∟B = 45°, СК - висота, СК = 7 см.
Знайдемо сторону АВ.
∆АВС - рівнобедрений (т. я. ∟A = ∟B).
В рівнобедреному ∆АВС висота СК, проведена до основи,
є медіаною i бісектрисою, тоді АК = КВ.
∟ACK = ∟KCB = 1/2∟ACB = 90° : 2 = 45° (СК - бісектриса ∟С).
Розглянемо ∆CKB - рівнобедрений (∟XCB = ∟KBC = 45°),
тоді СК = KB = 7 см. АК = KB = 7 см (СК - медіана).
АВ = АК + KB, АВ = 7 + 7 = 14 см.
Biдповідь: АВ = 14 см.