з геометрії 7 клас решебник відповіді

Вправа 242

 

Умова:

На сторонах АВ i ВС трикутника ABC подначили відповідно точки D i Е так, що ∟EAC = ∟DCA. Відрізки АЕ i CD перетинаються в точці F, DF = EF. Доведіть, що трикутник ABC рівнобедрений.

 

Відповідь:

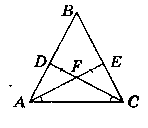
Доведения:
Нехай дано ∆АВС, ∟EAC = ∟DCA, АЕ i CD перетинаються в т. F,
DF = FE. Доведемо, що ∆АВС - рівнобедрений.
Розглянемо ∆FAC.
Так як ∟FAC = ∟FCA, то ∆FAC - рівнобедрений, тоді AF = FC.
Розглянемо ∆ADC i ∆СЕА.
1) ∟FAC = ∟DCA (за умовою).
2) АС - спільна.
3) АЕ = AF + FF, CD = CF + FЕ, так як AF = CF (∆FAC - рівнобедрений),
EF = FD (за умовою), тоді АЕ = CD.
Отже, ∆ADC = ∆СЕА за I ознакою piвностi трикутників.
3 цього випливає, що ∟DAC = ∟ECA.
Розглянемо ∆АВС.
Оскільки ∟BAC = ∟BCA, то ∆АВС - рівнобедрений.