Геометрія 7 клас

Вправа 258

 

Умова:

Кожна з точок М i N рівновіддалена від кінців відрізка АВ. Доведіть, що пряма MN - серединний перпендикуляр відрізка АВ.

 

Відповідь:

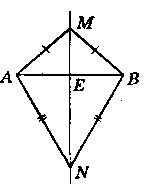
Дано: відрізок AB, AM = MB, AN = NB.
Довести: MN - серединний перпендикуляр.
Доведения: Розглянемо ∆NAM i ∆NBM.
1) AN = NB (за умовою); 2) AM = MB (за умовою); 3) NM - спільна сторона.
За III ознакою piвності трикутників маємо ∆NАМ = ∆NBM.
Отже, ∟AME = ∟BME, ∟ANE = ∟BNE (як piвність відповідних елементів рівних фігур).
Розглянемо ∆AMB - рівнобедрений (AM = MB).
Якщо ∟AME = ∟BME, тоді ME - бісектриса.
За властивістю рівнобедреного трикутника маємо ME - висота, медіана, ME ┴ АБ, АЕ = ЕВ.
Аналогично ∆ANB - рівнобедрений. ∟ANE = ∟BNE,
тоді NE - бісектриса, медіана, висота, NE ┴ АВ, АЕ = ЕВ.
Тоді маємо MN ┴ AB i MN ділить АВ навпіл.
Отже, MN - серединний перпендикуляр. Доведено.