Геометрія 7 клас

Вправа 262

 

Умова:

Відрізки BD i B₁D₁ - бісектриси трикутників ABC i A₁B₁C₁ відповідно, АВ = А₁В₁, BD = B₁D₁, AD = A₁D₁.
Доведіть, що ∆АВС = ∆A1B1C1.

 

Відповідь:

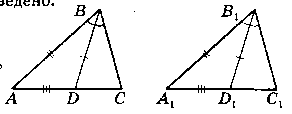
Дано: ∆АВС i ∆A1B1C1. BD - бісектриса ∆АВС, В₁D₁ - бісектриса ∆A1B1C1.
BD = B₁B₁, AD = A₁D₁ Довести: ∆АВС = ∆A1B1C1.
Доведення: Розглянемо ∆АВС i ∆A1B1C1.
За умовою АВ = A₁В₁, BD = В₁D₁, AD = A₁D₁.
За III ознакою piвностi трикутників маємо
∆ABD = ∆А₁B₁D₁. Звідси ∟ABD = ∟А1B1D1, ∟ADB = ∟A₁D₁B₁, ∟BAD = ∟B₁A₁D₁ (як piвнi елементи рівних фігyp).
За умовою BD - бісектриса ∟АВС. ∟ABD = ∟DBC, B₁D₁ - бісектриса ∟А1В1С1,
∟А1B1D1 = ∟D₁B₁C₁. Тому, якщо ∟ABD = ∟А1B1D1, тоді
∟ABC = ∟A1B1C1.
Розглянемо ∆BDC i ∆B₁D₁C₁.
За умовою BD = B₁D₁, ∟DBC = ∟D₁B₁C₁.
Якщо ∟ADB = ∟A₁D₁B₁, тоді ∟BDC = ∟D1B1C1 (суміжні кути piвним кутам).
За II ознакою pівності трикутників маємо
∆BDC = ∆B1D1C1. Звідси маємо DC = D₁C₁, AD = A₁D₁.
За аксіомою вимірювання відрізків маємо
AC = AD + DC i A₁C₁ = A₁D₁ + D₁C₁.
Розглянемо ∆АВС i ∆A1B1C1.
AB = A1B1, AC = A₁C₁, ∟ВAD = ∟B₁A₁D₁.
3a I ознакою piвностi трикутників маємо ∆АВС = ∆A1B1C1. Доведено.