Мерзляк Полонський Геометрія 7 клас відповіді гдз

Вправа 275

 

Умова:

Доведіть, використовуючи метод від супротивного, що коли жодна з висот трикутника не збігається з бiceктрисою, проведеною з тієї самої вершини, то трикутник не є рівнобедреним.

 

Відповідь:

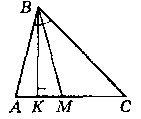
Доведения: Нехай дано ААВС, ВК - висота, ВМ - бкектриса,
доведемо, що ∆АВС не рівнобедрений.
Припустимо обернене: нехай ∆АВС - рівнобедрений.
Розглянемо ∆АВМ i ∆СВМ.
1) ∟ABM = ∟CBM (ВМ - бісектриса);
2) АВ = ВС (∆АВС - рівнобедрений);
3) ∟A = ∟C (∆АВС - рівнобедрений).
Отже, ∆АВМ = ∆СВМ за II ознакою, тоді ∟AMB = ∟CMB.
∟AMB + ∟CMB = 180° як cyміжні, з цього випливає, що ∟AMB = ∟CMB = 90°.
Тода MB - висота ∆АВС, але це суперечить умові бісектриса i висота не збігаються.
Тоді наше припущення неправильне, а правильне те, що треба було довести:
∆АВС не є рівнобедреним.