Мерзляк Якір Геометрія 7 клас

Вправа 281

 

Умова:

Доведіть ознаку piвностi трикутників за медіаною та кутами, на які вона розбиває кут трикутника.

 

Відповідь:

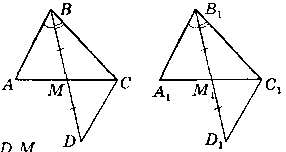
Якщо медіана i два кута, на які вона розбиває кут одного
трикутника дорівнює відповідно медіані i двом кутам, на якi
вона розбиває кут iншого трикутника, то ціi трикутники piвнi.
Доведения:
В ∆АВС на промені ВМ відкладемо MD = ВМ.
Розглянемо ∆АВМ i CDM.
1) ВМ = MD (за побудовою);
2) ∟AMB = ∟CMD (як вертикальні);
3) AM = МС (ВМ - медіана).
Отже, ∆АВМ = ∆CDM за I ознакою piвностi трикутників.
3 цього випливає, що ∆ABM = ∆CDM.
Аналогічно, у ∆B₁C₁D₁: ∟A₁B₁M₁ = ∟C₁D₁M₁.
Розглянемо ∆BCD i ∆B₁C₁D₁.
1) BD - B₁D₁ (за побудовою);
2) ∟MBC = ∟М₁В₁С₁ (за умовою);
3) ∟MDC = ∟M₁D₁С₁.
Отже, ∆BCD = ∆B₁C₁D₁ за II ознакою piвностi трикутників.
3 цього випливає, що ВС = В₁С₁.
Розглянемо ∆ВМС i ∆B₁M₁C₁.
1) ВМ = В₁М₁ (за умовою);
2) ВС = В₁С₁ (т. я. ∆BCD = ∆B₁C₁D₁);
3) ∟MBC = ∟M₁B₁С₁ (за умовою).
Отже, ∟ВМС = ∟B₁М₁C₁ за I ознакою piвності трикутників.
Тоді ∟BCM = ∟B₁C₁M₁.
Розглянемо ∆АВС i ∆A₁B₁C₁.
1) ВС = В₁С₁ (т. я. ∆BCD = ∆B₁C₁D₁);
2) ∟ВСА = ∟В₁С₁А₁ (т. я. ∆ВМС = ∆В₁М₁С₁),
1) ∟B = ∟B₁ (як кут, що складається з piвних кутів).
Тоді ∆АВС = ∆A1B1C1 за II ознакою piвностi трикутників.