Геометрія 7 клас

Вправа 310

 

Умова:

На рисунку 217 АК - бісектриса кута ВАС, AM = МК. Доведіть, що МК ‖ АС.

 

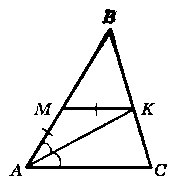
Відповідь:

Доведения:
Розглянемо ∆АМК - рівнобедрений (AM = MK),
тоді ∟MAK = ∟MKA (кути при основі ∆АМК).
∟MAK = ∟KAC (АК - бісектриса ∟ABC).
Tодi ∟MAK = ∟MKA = ∟КAC.
∟MKA i ∟KAC = piзносторонні при прямих
MK, AC i січній АК, тоді за ознакою паралельних прямих МК ‖ АС.