Геометрія 7 клас решебник відповіді
Вправа 321
Умова:
Відрізки AM i CK - медіани трикутника ABC. На продовженні відрізка AM за точку М відкладено відрізок MF, а на продовженні відрізка СК за точку К - відрізок KD так, що MF = АМ, KD = СК. Доведіть, що точки В, D i F лежать на одній прямій.
Відповідь:
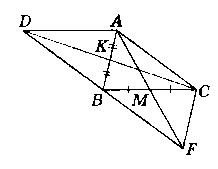
Доведения:
Нехай дано ∆АВС, AM - медіана, СК - медіана, AM = MF, СК = KD за побудовою.
Розглянемо ∆АМС i ∆FMB.
1) AM = MF (за побудовою);
2) ВМ = МС (AM - медіана);
3) ∟AMC = ∟FMB (як вертикальні).
Отже, ∆АМС = ∆FMB за I ознакою piвностi трикутників, з цього ви-
пливає, що ∆MAC = ∆MFB.
∆MAC i ∆MFB - різносторонні при прямих АС i BF та cічній AF.
Тоді за ознакою паралельності прямих AC ‖ BF.
Розглянемо ∆АКС i ∆BKD.
1) АК = ВК (СК - медіана);
2) СК = KD (за побудовою);
3) ∟AKC = ∟BKD (як вертикальні).
Отже, ∆АКС = ∆BKD за I ознакою piвностi трикутників, з цього випли-
ває, що ∟BDA = ∟ACD.
∟BDK i ∟АСК - різносторонні при прямих AC i BD та січній DC.
Тоді за ознакою паралельності прямих AC ‖ BD.
Оскільки BF ‖ АС i BD ‖ АС, то точки В, F, D лежать на одній прямій.
Повідомити про помилку
Обгрунтуй, що саме не так!




