Мерзляк домашня з геометрії 7 клас відповіді

Вправа 338

 

Умова:

На рисунку 233 АВ ‖ CD, ВС ‖ AD. Доведіть, що ВС = АВ.

 

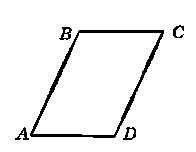
Відповідь:

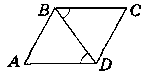
Дано:
АВ ‖ CD; ВС ‖ AD. Довести: ВС = AD.
Доведения:
Виконаємо додаткову побудову: січну BD.
За умовою ВС ‖ AD, BD - січна.
За ознакою паралельності прямих ∟CBD = ∟BDA (внутрішні різносторонні).
Аналогічно ∟ABD = ∟CDB (внутрішні різносторонні при прямих АВ ‖ CD, BD - січна).
Розглянемо ∆ABD i ∆СDB.
BD - спільна сторона; ∟ADB = ∟CBD; ∟ABD = ∟CDB.
За II ознакою piвностi трикутників маємо:∆ABD = ∆CDB.
Звідси AD = ВС (як piвні елементи рівних фігур).
Доведено.