Геометрія 7 клас Мерзляк решебник відповіді гдз

Вправа 341

 

Умова:

Через вершину В трикутника ABC (рис. 235) провели пряму МК, паралельну прямій AC, ∟MBA = 42°, ∟CBK = 56°. Знайдіть кути трикутника ABC.

 

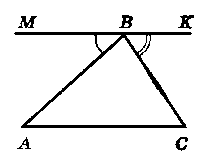
Відповідь:

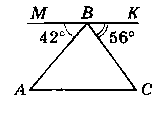
Дано:
∆АВС; МК ‖ АС; В є МК. ∟MBA = 42°; ∟CBK = 56°.
Знайти: кути ∆ABC.
Розв'язання: ∟MВK - розгорнутий.
За аксіомою вимірювання кутів маємо:
∟MBK = ∟MBA + ∟ABC + ∟CBK.
∟ABC = 180° - (42° + 56°) = 180° - 98° = 82°.
За умовою МК ‖ АС; ВС - січна.
За ознакою паралельності прямих маємо:
∟KBC = ∟ACB = 56° (внутрішні різносторонні).
Аналогічно МК ‖ АС; АВ - січна; ∟MBA = ∟BAC = 42°.
Biдповідь: ∟А = 56°; ∟C = 42°; ∟B = 82°.