Мерзляк Геометрія 7 клас

Вправа 346

 

Умова:

На рисунку 239 АВ = AC, AF = FE, AB ‖ EF. Доведіть, що АЕ ┴ ВС.

 

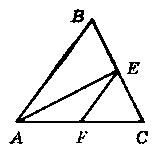
Відповідь:

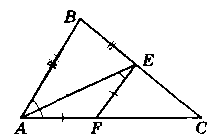
Дано:
∆АВС; АВ = AC; AF = FE; AB ‖ EF. Довести: АЕ ┴ ВС.
Доведения:
За умовою AF = FE, тому ∆AFE - рівнобедрений.
За властивістю кутів рівнобедреного трикутника маємо ∟FAE = ∟AEF.
За умовою АВ ‖ FE; АЕ - січна.
За ознакою паралельності прямих маємо:
∟BAE = ∟AEF (внутрішні різносторонні).
Якщо ∟BAE = ∟AEF i ∟EAF = ∟AEF.
Тому ∟BAE = ∟EAF, тодг АЕ - бісектриса ∟BAC.
За умовою АВ = AC, тоді ∆ВАС - рівнобедрений.
За властивістю piвнобедреного трикутника, якщо АЕ - бісектриса, тоді АЕ - висота. АЕ ┴ ВС.
Доведено.