Мерзляк Полонський Геометрія 7 клас решебник відповіді

Вправа 349

 

Умова:

На рисунку 241 АВ ‖ DE, ∟ABC = 120°, ∟CDE = 150°. Доведіть, що ВС ┴ CD.

 

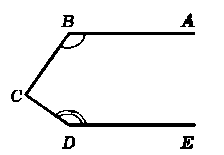
Відповідь:

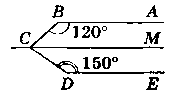
Дано:
АВ ‖ DE; ∟АВС = 120°; ∟CDE = 150°.
Довести: ВС ┴ CD.
Доведения:
Через точку С проведемо пряму CM ‖ DE; CM ‖ ВА.
Якщо ВА ‖ СМ; СВ - січна, тоді за ознакою паралельності прямих маємо:
∟АВС + ∟MCB = 180° (внутрішні односторонні).
∟MCB = 180° - 120° = 60°.
Якщо DE ‖ CM; CD - січна.
Аналогічно ∟MCD + ∟CDE = 180°;
∟MCD = 180° - 150° = 30°.
За аксіомою вимірювання кутів маємо:
∟BCD = ∟BCM + ∟MCD = 60° + 30° = 90°. Отже: ВС ┴ CD.
Доведено.