Мерзляк Полонський Геометрія 7 клас решебник
Вправа 351
Умова:
Через точку О перетину бісектрис АЕ i CF трикутника ABC провели пряму, паралельну прямій АС. Ця пряма перетинає сторону АВ у точці М, а сторону ВС - у точці К. Доведіть, що МК = АМ + СК.
Відповідь:
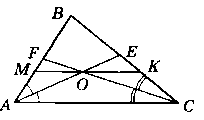
Дано:
∆АВС; АЕ - бісектриса ∆АВС;
CF - бісектриса ∆АВС; АЕ ∩ CF = 0. О ∩ МК; М є АВ; К є СВ. МК ‖ АС.
Довести: МК = AM + СК.
Доведения:
За умовою АЕ - бісектриса ∆АВС.
За означениям бісектриси кута трикутника маємо: ∟BAO = ∟OAC.
Аналогічно CF - бісектриса ∆АВС, тоді ∟ACO = ∟OCK.
За умовою МК ‖ АС; АО - січна.
За ознакою паралельності прямих маємо: ∟CAO = ∟AOM.
Звідси ∟OAM = ∟MOA. Toдi ∆АМО - рівнобедрений AM = МО.
Аналогічно МК ‖ АС; ОС - січна,
тоді ∟ACO = ∟СОК (внутрішні piзностороннi).
Звідси ∟OCK = ∟СОК, тому ∆ОКС - рівнобедрений. ОК = КС. МК = МО + ОК; МК = АМ + СК.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




