Мерзляк домашня з геометрії 7 клас решебник відповіді

Вправа 352

 

Умова:

Бісектриси кутів ВАС i ВСА трикутника ABC перетинаються в точці О. Через цю точку проведено прямї, які паралельні прямим АВ i ВС та перетинають сторону АС у точках М i К відповідно. Доведіть, що периметр трикутника МОК дорівнює довжині сторони АС.

 

Відповідь:

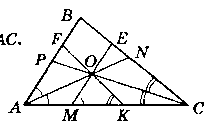
Дано:
∆АВС; AN, СР - бісектриси ∆АВС.
AN ∩ СР = 0. О є FK; О є ЕМ; М є АС; К є AC.
ЕМ ‖ АВ; FK ‖ ВС.
Довести: Р_∆МОК = АС.
Доведения:
За умовою AN - бісектриса ∆АВС.
За означенням бісектриси кута трикутника маємо: ∟BAN = ∟NAM.
АВ ‖ ME; АО - січна, тоді за ознакою паралельності прямих маємо:
∟РАО = ∟АОМ (внутрішні різносторонні).
Звідси ∟OAM = ∟МОА, отже ∆АМО - рівнобедрений AM = МО.
Аналогічно СР - бісектриса, тоді ∟АСР = ∟РСВ.
FK ‖ ВС; ОС - січна, тоді ∟КОС = ∟OCN.
Звідси ∟КОС = ∟КСО, тоді ∆КОС - рівнобедрений ОК = КС.
Р_∆МОК = МО + ОК + МК. Р_∆МОК = АМ + МК + КС = АС.
Доведено.