Мерзляк Якір Геометрія 7 клас решебник відповіді гдз

Вправа 354

 

Умова:

Відрізки AC i BD перетинаються в точці О, АВ = ВС = CD = AD. Доведіть, що АС ┴ BD.

 

Відповідь:

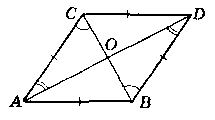
Дано:
АС ∩ BD = 0. AB = ВС = CD = AD.
Довести: AC ┴ BD.
Доведения:
Розглянемо ∆ADB i ∆CBD. За умовою AD = AB = CB = CD;
DB - спільна сторона.
За III ознакою piвності трикутників маємо: ∆ADB = ∆CBD,
звідси ∟ADB = ∟CBD (як piвнi елементи piвниx фігур).
Аналогічно ∆АВС = ∆CDB, звідси ∟DAC = ∟ACB.
Розглянемо ∆AOD i ∆СОВ. AD = ВС; ∟DAO = ∟OCB; ∟ODA = ∟OBC.
3a II ознакою piвності трикутників маємо: ∆AOD = ∆СОВ.
Звідси DO = OB. ∆DAB - рівнобедрений (AD = AB).
Якщо DO = OB; АО - медіана.
За властивістю рівнобедреного трикутника маемо: АО - висота,
тоді АО ┴ DB; AC ┴ DB.
Доведено.