з геометрії 7 клас

Вправа 372

 

Умова:

У рівнобедреному трикутнику ABC з кутом при вершині В, який дорівнює 36°, провели бісектрису AD. Доведіть, що трикутники ADB i CAD рівнобедрені.

 

Відповідь:

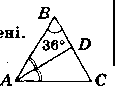
Доведения:
Нехай дано ∆АВС - рівнобедрений (АВ = ВС), ∟B = 36°, AD - бісектриса.
Доведемо, що ∆ABD i ∆BAC - рівнобедрені.
Розглянемо ∆АВС, так як АВ = ВС, то ∟A = ∟C.
Оскільки ∟A + ∟B + ∟C = 180°, то ∟A + ∟C + 36° = 180°;
∟A + ∟C = 144°; ∟A = ∟C = 144 : 2 = 72°.
∟BAD = ∟DAC = 72° : 2 = 36° (AD - бісектриса).
Розглянемо ∆ABD:
∟B = 36°, ∟BAD = 36°, тому ∆ABD - рівнобедрений з основою АВ.
Розглянемо ∆DAC: ∟C = 72°, ∟DAC = 36°.
Оскільки ∟C + ∟DAC + ∟CDA = 180°, то 72° + 36° + ∟CDA = 180°.
∟CDA = 180° - 108°; ∟CDA = 72°.
В ∆DAC: ∟C = 72°, ∟CDA = 72°, тому ∆DAC - рівнобедрений з основою DC.