Мерзляк Геометрія 7 клас
Вправа 388
Умова:
Знайдіть кути рівнобедреного трикутника, якщо один iз його зовнішніх кутів дорівнює: 1) 54°; 2) 112°. Скільки розв'язків має задача?
Відповідь:
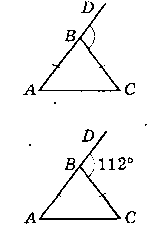
1) ∆АВС - рівнобедрений (AВ = ВС).
Зовнішній кут дорівнює 54°, тоді внутрішній буде тупий,
це не може бути кут при ocновi, так як в трикутнику не може
бути 2 тупих кута. (∟A = ∟C). Тому це кут при вершині В.
∟DBC = 54°. ∟DBC = ∟A + ∟C; 54° = ∟A + ∟C.
∟A = ∟C = 54° : 2 = 27°.
∟ABC = 180° - 54° = 126°.
Bідповідь: 27°; 27°; 126°.
2) а) ∆АВС - рівнобедрений (АВ = ВС).
Нехай зовнішній кут 112° - це кут при вершині В.
∟DBC = 112°, тоді ∟DBC = ∟A + ∟C;
112° = ∟A + ∟С; ∟B = 180° - 112° = 68°.
∟A = ∟C = 112° : 2 = 56
Biдповідь: 56°; 56°; 68°.
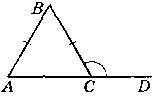
б) ∆АВС - рівнобедрений (АВ = ВС).
Нехай зовнішній кут 112° - це кут при основі ∟BCD = 112°, тоді
∟BCD + ∟BCA = 180°; ∟BCA = 180° - 112° - 68°.
∟BCA = ∟BAC = 68° (∆АВС - р1внобедрений).
∟BAC + ∟BCA + ∟B = 180°.
∟B = 180° - (68° + 68°) = 180° - 136° = 44°.
Biдповідь: 68°, 68°, 44°.
Повідомити про помилку
Обгрунтуй, що саме не так!




