Мерзляк домашня з геометрії 7 клас решебник гдз
Вправа 393
Умова:
Бісектриси кутів при основі АС рівнобедреного трикутника ABC перетинаються в точці О. Доведіть, що кут АОС дорівнює зовнішньому куту трикутника ABC при вершині А.
Відповідь:
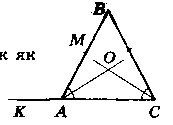
Доведения:
Нехай ∆АВС - рівнобедрений (АВ = ВС), АО - бісектриса, СО - бісектриса.
∟KAB - зовннішній кут ∆АВС, доведемо, що ∟AOC = ∟KAB.
Нехай ∟A = ∟C = х, тоді ∟KAB = 180° - х (властивість зовнішнього кута).
∟BAO = ∟OAC = ∟BCO = ∟OCA = 1/2∟A = 1/2∟C = х/2
(так як АО i СО - бісектриси рівних кутів).
Розглянемо ∆АОС.
∟ОАС + ∟АСО + ∟AOC = 180°.
х/2 + х/2 + ∟AOC = 180°; x + ∟AOC = 180°; ∟AOC = 180° - x.
Отже, ∟AOC = 180° - x i ∟KAB = 180° - x, тому ∟AOC = ∟KAB.
Повідомити про помилку
Обгрунтуй, що саме не так!




