Геометрія 7 клас решебник відповіді

Вправа 396

 

Умова:

На стороні АВ трикутника ABC позначили точку D так, що BD = ВС, ∟ACD = 15°, ∟DCB = 40°. Знайдіть кути трикутника ABC.

 

Відповідь:

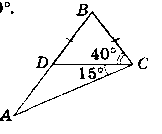
Розв язання.
Нехай даний ∆АВС, BD = ВС, ∟ACD = 15°, ∟DCB = 40°.
Знайдемо кути ∆АВС.
Розглянемо ∆DВС - рівнобедрений (BD = ВС), тоді
∟ВCD = ∟BDC = 40°.
Оскільки ∟B + ∟BCD + ∟BDC = 180°, то
∟B = 180° - (40° + 40°) = 100°; ∟C = ∟ACD + ∟DCB;
∟C = 15° + 40° = 55°.
Розглянемо ∆АВС:
∟A + ∟B + ∟C = 180°; ∟A + 100° + 55° = 180°;
∟A = 180° - (100° + 55°); ∟A = 25°.
Biдповідь: ∟A = 25°; ∟C = 55°; ∟B = 100°.