Мерзляк Геометрія 7 клас решебник

Вправа 398

 

Умова:

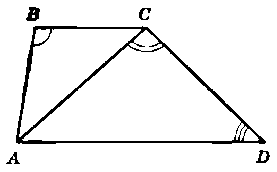
На рисунку 254 ВС ‖ AD, ∟B = 100°, ∟ACD = 95°, ∟D = 45°. Доведіть, що АВ = ВС.

 

Відповідь:

Доведения:
Розглянемо ∆ACD: ∟CAD + ∟D + ∟ACD = 180°;
∟CAD + 45° + 95° = 180°;
∟CAD = 180° - 140°; ∟CAD = 40°.
Так як ВС ‖ AD, то ∟BCA = ∟CAD - 40°
як різносторонні при ВС ‖ AD та січній AC.
Розглянемо ∆АВС: ∟ВАС + ∟В + ∟ВСА = 180°;
∟BAC + 100° + 40° = 180°; 
∟ВАС = 180° - 140°; ∟ВАС = 40°.
Оскільки в ∆АВС ∟ВСА = ∟ВАС = 40°,
то він рівнобедрений, тоді АВ = ВС.