з геометрії 7 клас відповіді гдз

Вправа 399

 

Умова:

Через вершину С трикутника ABC проведено пряму, яка паралельна бісектрисі AM трикутника й перетинає пряму АВ у точці К. Знайдіть кути трикутника АКС, якщо ∟BAC = 70°.

 

Відповідь:

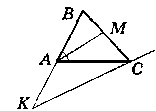
Нехай даний ∆АВС, ∟ВАС = 70°, AM - бісектриса, СК ‖ AM.
Знайдемо кути ∆КАС. ∟ВАС + ∟САК = 180° (кути суміжні);
∟САК = 180° - 70°; ∟САК = 110°.
Розглянемо AM ‖ КС i січну ВК, тоді ∟BAM = ∟BKC як відповідні.
∟BAM = ∟MAC = 1/2∟BAC = 70° : 2 = 35° (AM - бісектриса).
∟BAM = ∟BКC = 35°.
Розглянемо ∆AKC: ∟CAK + ∟AKC + ∟ACK = 180°;
110° + 35° + ∟ACK = 180°; 145° + ∟ACK = 180°;
∟ACK = 180° - 145°; ∟ACK = 35°.
Biдповідь: ∟CAK = 110°; ∟AKC = 35°; ∟ACК = 35°.