Геометрія 7 клас решебник

Вправа 400

 

Умова:

У трикутнику ABC бісектриси кутів А і С перетинаються в точці О. Знайдіть кут АОС, якщо ∟B = 100°.

 

Відповідь:

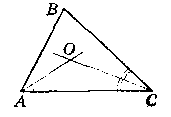
Нехай даний ∆АВС, АО - бісектриса, СО - бісектриса, ∟B = 100°.
Знайдемо ∟AOC.
Нехай ∟BAO = ∟OAC = х (АО - бісектриса).
∟BCO = ∟OCA = у (СО - бісектриса), тоді ∟A = 2х, ∟C = 2у.
Розглянемо ∆АВС:
∟A + ∟B + ∟C = 180°. 2х + 100 + 2у = 180;
2х + 2у = 180 - 100; 2х + 2у = 80; х + у = 40.
Розглянемо ∆АОС:
∟OAC + ∟OCA + ∟AOC = 180°.
х + у + ∟AOC = 180°; 40 + ∟AOC = 180;
∟AOC = 180° - 40° = 140°.
Biдповідь: ∟AOC = 140°.