Геометрія 7 клас

Вправа 403

 

Умова:

Кут при основі АС рівнобедреного трикутника ABC у 2 рази більший за кут при вершині, AM - бісектриса трикутника.
Доведіть, що ВМ = АС.

 

Відповідь:

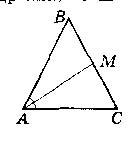
Доведения:
Нехай даний ∆АВС - рівнобедрений (АВ = ВС),
∟A у 2 рази більший ніж ∟B, AM - бісектриса.
Доведемо, що ВМ = АС.
Нехай ∟B = х, тоді ∟A = 2х, оскільки ∆АВС - рівнобедрений,
то ∟A = ∟C = 2х.
В ∆АВС: ∟A + ∟B + ∟C = 180°.
2х + х + 2х = 180; 5х = 180; х = 36.
∟B = 36°. ∟A = 2 • 36° = 72°. ∟C = 2 • 36° = 72°.
∟ВАМ = ∟MAC = 1/2∟A = 72° : 2 = 36° (AM - бісектриса).
Розглянемо ∆АВМ:
∟В + ∟ВМА + ∟ВАМ = 180°. 36° + ∟ВМА + 36° = 180°.
∟ВМА = 180° - 72° = 108°.
Отже, ∟В = ∟ВАМ = 36°, тоді ∆АВМ - рівнобедрений, ВМ = AM.
Розглянемо ∆АМС:
∟MAC + ∟АМС + ∟С = 180°.
36° + ∟АМС + 72° = 180°.
∟АМС = 180° - (36° + 72°) = 72°.
Так як ∟АМС = ∟С = 72°, то ∆АМС - рівнобедрений, МА = АС.
Оскільки, ВМ = MA, MA = АС, то ВМ = АС.