Геометрія 7 клас

Вправа 408

 

Умова:

У трикутнику ABC кут В тупий. На продовженні сторони АВ за точку А позначили довільну точку D. Доведітъ, що CD > AC.

 

Відповідь:

Доведения:
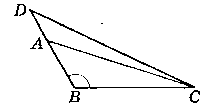
Нехай дано ∆АВС, ∟B тупий, т. D доведемо, що CD > АС.
Розглянемо ∆АВС.
Оскільки ∟B - тупий, то ∟A i ∟C - гострi.
∟DAC i ∟A - суміжні. Якщо ∟A - гострий, то ∟DAC - тупий.
Розглянемо ∆DAC - тупокутний (∆DAC - тупий), тоді ∆D i ∆DCA - гострi.
Сторона DC лежить напроти тупого кута DAC, а сторона АС лежить
напроти гострого кута D.
Отже, більшою є та сторона, яка лежить напроти більшого кута: CD > AC.