Мерзляк Геометрія 7 клас відповіді гдз

Вправа 417

 

Умова:

Відрізок AM - медіана трикутника ABC, ∟САМ > ∟BAM. Доведіть, що АВ > АС.

 

Відповідь:

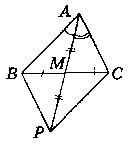
Доведения:
Нехай даний ∆АВС, AM - медіана, ∟САМ > ∟ВАМ.
Доведемо, що АВ > АС.
Продовжимо медіану AM за точку М на її довжину.
AM = MP.
Розглянемо ∆АМС i ∆РМВ:
1) AM = MP (за побудовою);
2) ВМ = МС (AM - медіана);
3) ∟AMC = ∟PMB (як вертикальні).
Отже, ∆АМС = ∆РМВ за I ознакою piвностi трикутників.
Розглянемо ∆РАС i ∆АРВ:
1) АС = ВР (∆АМС = ∆РМВ);
2) ∟PAC = ∟APB (∆АМС = ∆РМВ);
3) АР - спільна.
Отже, ∆РАС = ∆АРВ за I ознакою piвностi трикутників, з цього випливає
piвність вcix відповідних елементів:
∟APC = ∟ВАМ, АВ = PC.
Розглянемо ∆АРС:
∟РАС > ∟АРС, тоді PC > АС, так як АВ = PC, то АВ > АС.