Мерзляк Якір Геометрія 7 клас решебник
Вправа 419
Умова:
У трикутнику ABC відомо, що АВ = 2 см, ∟A = 60°, ∟B = 70°. На стороні АС позначили точку D так, що AD = 1 см. Знайдіть кути трикутника ВВС.
Відповідь:
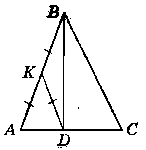
Нехай даний ∆АВС, ∟A = 60°, ∟B = 70°, АВ = 2 см, AD = 1 см.
Знайдемо кути ∆BDC.
В ∆ABD проведемо медіану DK.
АК = КВ = 1/2АВ = 2 : 2 = 1см.
Розглянемо ∆AKD - piвнобедрений (AD = АК = 1 см),
Якщо ∟A = 60°, то ∆AKD - piвносторонній.
Отже, AD = АК = KD, ∟А = ∟AКD = ∟KDA = 60°.
∟ВКD i ∟AKD - суміжні, тоді ∟BKD + ∟AKD = 180°.
∟BKD = 180° - 60° = 120°.
∆BKD - рівнобедрений (KB = KD = 1 см), тоді
∟KBD = ∟KDB = (180° - 120°) : 2 = 30°.
Розглянемо ∆АВС:
∟A + ∟B + ∟C = 180°. ∟C = 180° - (60° + 70°); ∟C = 50°.
∟B = ∟KBD + ∟DBC; ∟DBC = 70° - 30° = 40°.
Розглянемо ∆BDC:
∟DBC + ∟C + ∟BDC = 180°.
40° + 50° + ∟BDC = 180°. ∟BDC = 180° - 90° = 90°.
Biдповідь: ∟BDC = 90°; ∟DBC = 40°; ∟C = 50°.
Повідомити про помилку
Обгрунтуй, що саме не так!




