Геометрія 7 клас

Вправа 433

 

Умова:

Із точок A i В, які лежать в одній півплощині відносно прямої а, опущено перпендикуляри AM i BK на цю пряму, АМ = ВК. Доведіть, що АК = ВМ.

 

Відповідь:

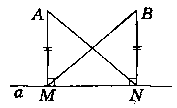
Дано:
A i В лежать в одній піплощині відносно прямої a;
AM ┴ а; ВК ┴ а. AM = ВК. Довести: АК = ВМ.
Доведения:
За умовою AM ┴ а, тоді ∟АМК = 90°.
Аналогічно, якщо ВК ┴ а, тоді ∟ВКМ = 90°.
Розглянемо ∆АМК i ∆ВКМ:
1) ∟АМК = ∟BКM = 90°;
2) AM = BК (за умовою);
3) МК - спільна сторона.
За ознакою piвності прямокутних трикутників маємо: ∆АМК = ∆ВКМ.
Звідси АК = ВМ (як piвнi елементи piвниx фігyp).
Доведено.