Геометрія 7 клас решебник гдз

Вправа 436

 

Умова:

Ha бісектрисi кута з вершиною в точці В позначили точку М, з якої опустили перпендикуляри MD i МС на стороні кута. Доведіть, що MD = МС.

 

Відповідь:

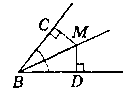
Дано:
∟B, MB - бісектриса ∟В; МС ┴ ВС; MD ┴ BD.
Довести: МС = МD.
Доведения:
За умовою МС ┴ СВ; ∟MCB = 90° i MD ┴ BD, ∟MDB = 90°.
За умовою MB - бісектриса ∟CBD.
За означенням бісектриси кута маємо: ∟MBC = ∟MBD.
Розглянемо ∆МСВ i ∆MDC:
1) ∟MCB = ∟MDB = 90°;
2) ∟MBC = ∟MBD;
3) MB - спільна сторона.
За ознакою piвностi прямокутних трикутників маємо: ∆МСВ = ∆MDB.
Звідси МС = MD (як piвнi елементи piвниx фігyp).
Доведено.