Геометрія 7 клас відповіді
Вправа 438
Умова:
Доведіть, що висоти рівнобедреного трикутника, проведені до його бічних сторін, є рівними.
Відповідь:
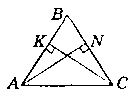
Дано:
∆АВС - рівнобедрений. АВ = ВС; AN, СК - висоти; AN ┴ ВС, СК ┴ АВ.
Довести: AN = СК.
Доведения:
За умовою ∆АВС - рівнобедрений (АВ = ВС).
За властивістю кутів при ocновi рівнобедреного трикутника маємо: ∟BAC = ∟BCA.
За умовою AN ┴ ВС; ∟ANC = 90°; СК ┴ АВ, ∟CКA = 90°.
Розглянемо ∆АКС i ∆CNA:
1) ∟ANC = ∟CКA = 90;
2) ∟BAC = ∟BCA;
3) AC - спільна сторона.
За ознакою piвностi прямокутних трикутників маємо: ∆АКС = ∆CNA.
Звідси AN = СК (як piвнi елементи рівних фігур).
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




