Мерзляк домашня з геометрії 7 клас

Вправа 453

 

Умова:

Кути ABC i DBC - суміжні, промінь BM належить куту ABC, промінь ВК - куту DBC, ∟MBC = ∟CBK = 30°, кут DBK у 5 разів больший за кут АВМ. Знайдітъ кути ABC i DBC.

 

Відповідь:

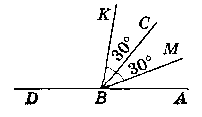
Дано:
∟DBC i ∟ABC - суміжні. Промінь ВМ проходить між сторонами ∟СВА.
Промінь ВК проходить між сторонами ∟АВС.
∟MBC = ∟CBK = 30°. ∟DBK > ∟ABM у 5 раз1в.
Знайти: ∟ABC i ∟DBC.
Розв'язання:
Нехай ∟ABM = х, тоді ∟DBK = 5х.
За аксіомою вимірювання кутів маємо:
∟DBC = ∟DBK + ∟KBC; ∟DBC = 5х + 30; ∟CBA = ∟CBM + ∟MBA; ∟CBA = x + 30.
За умовою ∟DBC i ∟CBA - суміжні.
За теоремою про суміжні кути маємо: ∟DBC + ∟CBA = 180.
Складемо i розв'яжемо рівняння:
5х + 30 + х + 30 = 180; 6х + 60 = 180; 6х = 180 - 60; 6х = 120; х = 20.
∟DBC = 5 • 20° + 30° = 100° + 30° = 130°. ∟CBA = 20° + 30° = 50°.
Biдповідь: 130°; 50°.