Мерзляк Якір Геометрія 7 клас

Вправа 469

 

Умова:

У трикутнику ABC відомо, що ∟C = 90°, ∟B = 30". Серединний перпендикуляр відрізка АВ перетинає його в точці М, а відрізок ВС - у точці К. Доведіть, що МК = 1/3ВС.

 

Відповідь:

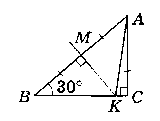
Нехай ∆АВС - прямокутний (∟C = 90°), ZB = 30°, МК - серединний перпендикуляр до сторони АВ.
Доведемо, що МК = 1/3ВС.
Розглянемо ∟АВС (∟C = 90°).
Оскільки ∟B = 30°, то АС = 1/2АВ.
МК - серединний перпендикуляр до АВ, тобто ВМ = МА = 1/2АВ і МК ┴ АВ.
Так як АС = 1/2АВ i ВМ = 1/2АВ, то АС = ВМ = МА.
Проведемо АК i розглянемо ∆АМК i ∆АСК:
1) ∟AMK = ∟АСК = 90° (за умовою);
2) АК - спільна;
3) AM = AC (iз попереднього).
Отже, ∆АМК = ∆АСК за катетом i гіпотенузою, тоді МК = КС.
Нехай МК = КС = х.
Розглянемо ∆ВМК (∟M = 90°): ∟B = 30°, тоді МК = -ВК,
ВК = 2 • МК = 2х. Так як т. А: належить відрізку ВС, то ВС = ВК + КС;
ВС = 2х + х = 3х; МК = х. Отже, МК = 1/3ВС.