Геометрія 7 клас решебник відповіді

Вправа 471

 

Умова:

У трикутнику ABC відомо, що ∟C = 90°, ∟BAC = 60°, відрізок AD - бісектриса, відрізок CD на 3 см менший від відрізка BD. Знайдіть бісектрису AD.

 

Відповідь:

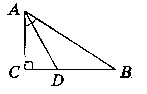
Нехай даний ∆АВС, ∟C = 90°, ∟BAC = 60°, AD - бісектриса,
CD менше ніж BD на 3 см. Знайдемо AD.
Оскільки AD - бісектриса ∟CAB, то:
∟CAD = ∟DAB = 1/2∟CAB = 60° : 2 = 30°.
Розглянемо ∆АВС (∟C = 90°):
∟CAB + ∟B = 90°; ∟B = 90° - 60° = 30°.
Розглянемо ∆ADB: ∟B = 30°, ∟DAB = 30°,
тоді ∆ADB - рівнобедрений AD = DB.
Нехай CD = х (см), тоді DB = х + 3 (см).
Розглянемо ∆ACD (∟C = 90°): CD - катет,
що лежить напроти ∟CAD = 30°,
тоді CD = 1/2AD; AD = 2 CD, AD = 2x (см).
Оскільки AD = DB, то DB = 2x (см).
Але DB = x + 3 (см); 2x = x + 3; х = 3.
AD = 2 • 3 = 6 см.
Biдповідь: AD = 6 см.