Мерзляк Полонський Геометрія 7 клас решебник відповіді
Вправа 499
Умова:
Відрізок AB - діаметр кола, М - довільна точка кола, відмінна від точок A i В. Доведіть, що ∟AMB = 90°.
Відповідь:
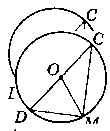
Дано:
Коло з центом О. М належить колу. АВ - діаметр.
Довести: ∟AMB = 90°.
Доведения:
Виконаємо додаткову побудову - радіус ОМ.
∆АОМ - рівнобедрений (АО = ОМ - радіуси).
За властивістю кутів рівнобедреного трикутника маємо ∟OAM = ∟ОМА.
Нехай ∟ОАМ = х, тоді ∟OMA = х.
За теоремою про суму кутів трикутника маємо
∟АОМ = 180° - (х + х) = 180° - 2х. ∟АОМ i ∟MOB - суміжні.
За теоремою про суміжні кути маємо:
∟MOB = 180° - (180° - 2х) = 180° - 180° + 2х = 2х.
Розглянемо &МОВ - рівнобедрений (ОМ = ОВ - радіуси).
∟ОВМ = ∟ОМВ = (180° - 2х) : 2 = 90° - х.
За аксіомою вимірювання кутів маємо:
∟АМО + ∟ОМВ = ∟АМВ; ∟АМВ = х + 90° - х = 90°.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




