Мерзляк домашня з геометрії 7 клас решебник відповіді
Вправа 502
Умова:
У рівнобедреному трикутнику ABC з основою АС проведено бісектриси AD i СЕ. Доведіть, що АЕ = ED.
Відповідь:
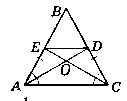
Дано:
∆ABC - рівнобедрений. АС - основа, AD - бісектриса ∟ВАС, СЕ - бісектриса ∟АСВ.
Довести: АЕ = ED.
Доведения:
Розглянемо ∆АВС - рівнобедрений (АВ = ВС).
За властивістю кутів рівнобедреного трикутника маємо: ∟ВАС = ∟ВСА.
За умовою AD - бісектриса ∟ВАС, тоді ∟BAD = ∟DАС = 1/2∟ВАС.
Аналогічно СЕ - бісектриса ∟BCA, тоді ∟BCE = ∟ECA = 1/2∟BCA.
Нехай ∟ECA = ∟CAD = ∟DAE = х, тоді ∟CAE = 2х.
Розглянемо ∆САЕ.
За теоремою про суму кутів трикутника маємо:
∟CEA = 180° - (х + 2х) = 180° - 3х.
Розглянемо ∆АОЕ.
За теоремою про суму кутів трикутника маємо:
∟EOA = 180° - (180° - 3х + х) = 180° - 180° + 3х - х = 2х.
∟AOE i ∟EOD - суміжні.
За теоремою про суміжні кути маємо:
∟EOA = 180° - 2х.
∆EOD - рівнобедрений.
Тому ∟OED = ∟ODE = (180° - (180° - 2x)) : 2 =
= (180° - 180° + 2x) : 2 = (2x) : 2 = x. Отже, ∟EAO = ∟ODE.
Тому ∆AED - рівнобедрений.
Отже, АЕ = ED.
Доведено.
Повідомити про помилку
Обгрунтуй, що саме не так!




