Геометрія 7 клас гдз
Вправа 512
Умова:
Доведіть, що piвнi хорди кола рівновіддалені від його центра.
Відповідь:
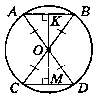
Нехай дано коло (О; R), АВ i CD - хорди, АВ = CD.
Доведемо, що відстань від хорди АВ i від хорди CD до центра piвнi.
Розглянемо ∆ЛОВ i ∆DOC.
1) АО = OD
} як радіуси кола.
2) ВО = СО
3) АВ = CD (за умовою).
Отже, ∆АОВ = ∆DOC за III ознакою piвностi трикутників.
Проведемо OK ┴ AB i ОМ ┴ CD.
∆ЛОВ i ∆COD - рівнобедрен1і (АО = ОВ = СО = OD = R).
3 цього випливає, що ∟A = ∟B = ∟C = ∟D.
Розглянемо ∆АОК i ∆DOM.
1) АО = OD (як радіуси).
2) ∟А = ∟D (∆АОВ = ∆DOC).
3) ∟AKO = ∟DMO = 90° (ОК ┴ АВ, ОМ ┴ CD).
Отже, ∆АОК = ∆DOM за гіпотенузою і гострим кутом.
Тоді ОК = ОМ. ОК - відстань від т. О до АВ.
ОМ - відстань від т. О до CD.
Повідомити про помилку
Обгрунтуй, що саме не так!




