Мерзляк Полонський Геометрія 7 клас відповіді

Вправа 524

 

Умова:

Через кінці хорди АВ, яка дорівнює радіусу кола, проведено дві дотичні, що перетинаються в точці С. Знайдіть кут АСВ.

 

Відповідь:

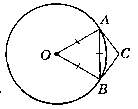
Нехай дано коло(0; R), АВ - хорда, АВ = АО = OB = R. AC i СВ - дотичні.
Знайдемо ∟ACB.
Розглянемо ∆ОАВ - рівносторонній (ОА = ОВ - АВ = R),
тоді ∟AOB = ∟ABO = ∟BAO = 60°.
Оскільки СА - дотична, ОА - радіус, А - точка дотику, то СА ┴ ОА.
∟OAC = 90°. ∟BAC = 90° - 60°; ∟BAC = 30°.
Розглянемо ∆АСВ - рівнобедрений (АС = ВС як відрізки дотичних, проведених
з однією точки до кола), тоді ∟CAB = ∟CBA = 30°.
∟CAB + ∟CBA + ∟ACB = 180°;
∟ACB = 180° - (30° + 30°);
∟ACB = 180° - 60° = 120°.
Biдповідь: ∟ACB = 120°.