Геометрія 7 клас решебник відповіді гдз

Вправа 527

Умова:

Відрізки АВ i ВС - відповідно хорда й діаметр кола, ∟АВС = 30°. Через точку А проведено дотичну до кола, яка перетинає пряму ВС у точці D. Доведіть, що трикутник ABD pівнобедрений.

Відповідь:

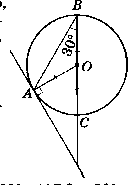
Нехай дано коло (О; R), АВ - хорда, ВС - діаметр, ∟ABC = 30°,
AD - дотична, дотична i діаметр перетинаються в т. D.
Доведемо, що ∆ABD - рівнобедрений.
Розглянемо ∆АОВ - рівнобедрений (АО = OB = R).
∟ABO = ∟OAB = 30°; ∟ABO + ∟OAB + ∟AOB = 180°;
∟AOB = 180° - (30° + 30°); ∟AOB = 120°.
ОА - радіус, проведений в точку дотику, за властивістю дотичної ОА ┴ AD. ∟OAD = 90°.
Розглянемо ∆AOD (∟OAD = 90°). ∟AOB + ∟AOD = 180° (як суміжні).
∟AOD = 180° - 120° = 60°; ∟AOD + ∟ADO = 90°; ∟ADO = 90° - 60° = 30°.
Розглянемо ∆ABD.
∟ABD = 30°, ∟ADO = 30°. Тоді ∆ABD - рівнобедрений з основою BD.