Мерзляк Якір Геометрія 7 клас відповіді гдз

Вправа 532

 

Умова:

Прямі, які дотикаються до кола iз центром О в точках А i В, перетинаються в точці К, ∟AKB = 120°.
Доведіть, що АК + ВК = ОК.

 

Відповідь:

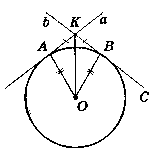
Нехай дано коло (О; R), пряма a i пряма b - дотичні, т. A i В - точки дотику.
Пряма a i пряма b перетинаються в т. К, ∟AKB = 120°.
Доведемо, що АК + ВК = ОК.
ОА i OB - радіуси, які проведені в точки дотику,
за властивістю дотичної ОА ┴ АК, OB ┴ KB.
Розглянемо ∆АКО i ∆BKO.
1) ∟KAO = ∟KBO = 90° (OA ┴ AK, OB ┴ BK).
2) АО = OB (як радіуси).
3) КО - спільна.
Отже, ∆АКО = ∆ВКО за катетом i гіпотенузою,
з цього випливає, що ∟АКО = ∟BKO.
∟AKO = ∟BKO = 1/2∟AKB = 120° : 2 = 60°.
Розглянемо ∆АКО (∟CAO = 90°).
∟AKO + ∟AOK = 90°; ∟AOK = 90° - 60° = 30°.
Тоді катет АК, що лежить напроти кута 30°,
дорівнює половині гіпотенузи КО. АК = 1/2КО.
Аналогічно, з ∆КВО (∟KBO = 90°)
КВ = 1/2КО; АК + КВ = 1/2КО + 1/2 КО = КО.