Геометрія 7 клас решебник

Вправа 533

 

Умова:

Коло дотикається до сторони АВ трикутника ABC у точці М i дотикається до продовження двох інших cтopiн. Доведіть, що сума довжин відрізків ВС i BM дорівнює половині периметра трикутника ABC.

 

Відповідь:

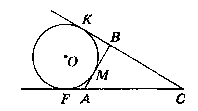
Нехай дано ∆АВС, коло (О; R), коло дотика'ться сторони АВ в т. М,
продовження сторони СВ в т. К, продовження сторони СА в т. F.
Доведемо, що ВС + ВМ = 1/2Р_∆АВС.
За властивістю відрізків дотичних, проведених з однієї точки до кола:
ВМ = ВК = х; АМ = AF = z; КС = FC = у;
Р_∆АВС = АВ + ВС + АС; АВ = AM + MB = z + х; ВС = КС - KB = у - х;
АС = FC - FA = у - z.
Р_∆АВС = z + x + y - x + y - z = 2y; BC + ВМ = у - х + z - у;
ВС + ВМ = 1/2Р_∆АВС.